Incremental computation is a way of performing computations, with the expectation of future changes in the inputs to the computiation. When those changes occur the output can be updated efficiently, at minimum faster than redoing the whole computation from scratch.

This problem occurs in many programming domains - UI programming, data flow, build systems, compilers, code editors. Likely you have seen it before, but didn’t call it incremental computation. Despite its prevalence, it is rarely viewed as a common computational paradigm. It is more often referred to as an ad-hoc application of caching or memoization. In comparison, other computational paradigms like concurrent, lazy, distributed computation have better known nomenclature and techniques.

In this series of blog posts I will attempt to teach you what ‘incremental computation’ is. I will motive the problem using a small subset of JavaScript and establish common terminology for the basic approaches to the problem. I spent the last few years surveying various academic and industry work that relate to incremental computation, resulting in diverse pool of prior work. I hope by the end of your reading of this post that work is accessible to you.

Motivation

To introduce ‘incremental computation’ I will start with intentionally limited environment that only contains functions and immutable primitives (numbers in this case). Jumping straight into a full featured programming language will obscure the core ideas. In a more formal setting this would be the lambda calculus, but I will just use TypeScript and just stay away from higher-level constructs like arrays. You can replace this with any run-of-the-mill programming language that has closures.

Let’s start with a very simple computation:

function d(x: number, y: number) {
  return Math.sqrt(x * x + y * y);
}

const computation = d(1, 2);

Incremental computation, ultimately, is concerned with the question how to most effectively re-compute d(x, y) when some of the inputs have changed from 1 and 2 to something else.

Say the new computation I would like to execute is d(1, 3). The new inputs do not fully match the old ones, so a simple caching will not work as written.

However, instead of giving up on caching, I can break down the computation down to the basic operations: addition, multiplication and square root.

There are four core operations performed - two multiplications, one addition and one Math.sqrt. I call the basic building blocks of a computation - operations, but note that this is not standard. To spell it out using temporary variables:

const op1 = 1 * 1;
const op2 = 2 * 2;
const op3 = op1 + op2;
const op4 = Math.sqrt(op3);

Compare now with the version with the new inputs.

const op1 = 1 * 1;
const op2 = 3 * 3;
const op3 = op1 + op2;
const op4 = Math.sqrt(op3);

For this toy example, the best incremental computation will reuse or skip 1 * 1 and then redo the other three operations with the new inputs.

This can be easily expressed in an abstract directed graph form. The original computation is:

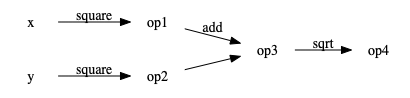
Each node represents a variable along with the computation needed to obtain in and all incoming edges together represent the inputs to the function that computes the variable.

The recomputation for d(1, 3) after d(1, 1) will ideally only go through the path in red.

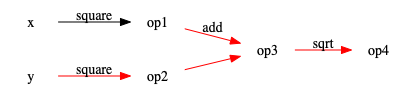
Meanwhile, the recomputation for d(-1, -1) after d(1, 1) will go start with two red paths, but end in the middle, since -1^2 == 1^2 the result doesn’t change.

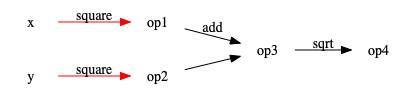
The basic algorithm of incremental computation over the abstract computation graph is:

Basic Algorithm of Incremental Computation

1. when at least one of the inputs of an operation has changed, redo the operation to get new outputs.
2. repeat until there are no more changes.

This algorithm is so simple that it has no name. The complexity comes in how to best build the computation graph, especially on top of general programming languages which have no incremental primitives.

The key questions around incremental computation at the abstract level of the computation graph will be:

• how is this computation graph built?
• how is the graph traversed. The Basic Algorithm in intentionally vague around that.
• can it change while the program is running?
• what if it has cycles?

The questions that I view secondary to the core and not going to explore at detail:

• who does the recomputation
• where is the data stored
• can it be parallelized across different processes

Memoization

At this simple form incremental computation seems to be connected to function memoization. Memoization is comparing the inputs of a function against a cache of (inputs, output) pairs. If seen, the function body is skipped and output used, otherwise the function body executes and the output is stored in the cache.

Incremental computation usually is concerned with the recomputation against a single past result, which would make it most fitting to use memoization with a cache size of one. I view basic caching considerations - like size of cache, least-frequently-used vs other strategies, orthogonal to the core problems of incremental computation.

In order to apply memoization to the computatation above, we have to first rewrite the function to separate the basic operations. This is known as A-normal form in the compiler literature.

function d(x: number, y: number) {
  const op1 = x * x;
  const op2 = y * y;
  const op3 = op1 + op2;
  const op4 = Math.sqrt(op3);
  return op4;
}

Now, we can memoize each inner operation along with the whole function:

const memoAdd = memo(add);
const memoSquare = memo(square);
const memoSqrt = memo(Math.sqrt);

function innerMemoD(x: number, y: number) {
  const op1 = memoSquare(x);
  const op2 = memoSquare(y);
  const op3 = memoAdd(op1, op2);
  const op4 = memoSqrt(op3);
  return op4;
}
const memoD = memo(innerMemoD);

This is admittedly, much more efficient and but I claim it is not the end of the story for incremental computation. Notice that while each operation is memoized - the computation proceeds exactly the same way as before through the computation graph:

We made the cost of each operation as small as possible during the evaluation, but the flow is always the same.

Beyond memoization

Let’s try to change the computation graph flow during recomputation. We can start by manually adding some ‘skip to the end’ calls:

let lastOp1: null|number = null;
let lastOp2: null|number = null;
let lastOp3: null|number = null;
let lastOp4: null|number = null;

function skipCallsD(x: number, y: number) {
  const op1 = memoSquare(x);

  // why not 'if op === lastOp1 -> skip' here?
  const op2 = memoSquare(y);

  if (op1 === lastOp1 && op2 === lastOp2) return lastOp4;
  lastOp1 = op1; lastOp2 = op2;

  const op3 = memoAdd(op1, op2);

  if (op3 === lastOp3) return lastOp4;
  lastOp3 = op3;

  const op4 = memoSqrt(op3);
  lastOp4 = op4;

  return op4;
}

Notice that the structure of the checks matches the abstract computation graph. We can’t skip to the end if op1 hasn’t changed, because potentially op2 can be different.

This implementation allows us to achieve the incremental flow depicted here for recomputing d(-1,-1) after d(1, 1)

But will not as written help with recomputing d(1, 3) after d(1, 1).

You should begin to see how to achieve “full incrementality” in the computation graph model. At each node if all inputs are unchanged we can skip until the next multi-input node or end of the computation if there are none. This is simply a restatement of the basic algorithm using the observation that a single input computation chain can be skipped to its end upon the first repeated output.

To make the example above fully incremental requires adding lastX and lastY and the following checks (at the right places):

if (x === lastX && y === lastY) return lastOp4;  // memoization condition
...
if (op1 === lastOp1 && y === lastY) return lastOp4;

Notice how much has our simple one-line function d has grown in size to achieve incrementality. Also unlike memoization it is not clear how precisely to mechanically add the if-else checks.

Next we will try to change the shape of the code. As it turns out the direct style of computation only one amongst many different ways for computation to look like. For each of those we will add incrementality. The hope is that the reshaping makes it easier to add incrementality.

Direct versus Reversed Computation

The program we have had so far was written in direct style. Each operation is done in order op1,op2,op3,op4 and each reads the variables it needs.

We can reverse the computation flow by imagining starting with op4, which in turn would need to compute op3 which will need op1 and op2. At the end we have x and y which are inputs to the computation.

Giving simple wrapper classes around these concepts - Input, SingleInputCmp and DoubleInputCmp, the computation can look something like:

// computation description
const x = new Input(1);
const y = new Input(1);
const op1 = new SingleInputCmp(square, x);
const op2 = new SingleInputCmp(square, y);
const op3 = new DoubleInputCmp(add, op1, op2);
const op4 = new SingleInputCmp(Math.sqrt, op3);

// computation
op4.get();

The arguments to each *Cmp class are pure functions to do the operation (like square or add) and one or two inputs depending on what is needed for the operation. The interesting part is that now the computation is described in code first and only afterwards “executed” in a reversed “output-to-input” fashion.

The rest of the code can be simply implemented like (apologies for folks that prefer not to use classes in TypeScript):

interface Var {
  get(): number;
}

class Input implements Var {
  constructor(private val: number) {}
  set(x: number) {
    this.val = x;
  }
  get(): number {
    return this.val;
  }
}

class SingleInputCmp implements Var {
  constructor(private readonly cmp: (x: number) => number,
              private readonly input: Var) {}
  get(): number {
    return this.cmp(this.input.get());
  }
}

class DoubleInputCmp implements Var {
  constructor(private readonly cmp: (x: number, y: number) => number,
              private readonly input1: Var,
              private readonly input2: Var) {}
  get(): number {
    return this.cmp(this.input1.get(), this.input2.get());
  }
}

So we reshaped the computation, but did it make it easier to add incrementality? As it turns out the answer is ‘no’. If we notice that op1 and op2 are the same and want to jump to the old output that would require skipping over op3 which was on the function call stack. We have to keep a custom stack in order to achieve this, so I will leave this as an exercise to the reader. You can see a gist to my solution (here)[https://gist.github.com/rkirov/1e002748a9794b098f39c918d191f59b].

Next we will look at another classic transformation of the computation model - continuation passing style.

Incremental Computation and Continuation Passing Style

If you have never seen it before, it can be explained with a bit of insight from the lambda calculus on top of our previous rewriting into basic operations (the A-normal form). Each variable assignment let x = <init>; <rest> can be written as ((x) => <rest>)(<init>). The (x) => <rest> function is called the continuation. In a slight modification from traditional CSP transform where the continuation is further passed into all other functions, we will skip that part.

We will do this transformation step-by-step:

function cspD(x: number, y: number) {
  return ((op1: number) => 
    ...
  )(square(x));
}

then add op2,

function cspD(x: number, y: number) {
  return ((op1: number) => 
    ((op2: number) =>
      ...
    )(square(y))
  )(square(x));
}

and eventually get to

function cspD(x: number, y: number) {
  return ((op1: number) => 
    ((op2: number) =>
      ((op3: number) =>
        ((op4: number) =>
          op4 
        )(Math.sqrt(op3))
      )(add(op1, op2))
    )(square(y))
  )(square(x))
}

Now let’s try to add incrementality. Given than we see a four new functions imagine memoizing them.

While it will give us the correct recomputation of d(-1,-1) after d(1,1) it will be wrong for d(1, 3) after d(1, 1). This is because as soon as op1 is the same as before we will skip to the end, ignoring any change to op2.

The correct rewriting for memoization requires to preserve the fact op3 has two inputs over which we have to memoize together. This looks like:

function insideOutD(x: number, y: number) {
  return ((op1: number, op2: number) => 
    ((op3: number) =>
      ((op4: number) =>
        op4 
      )(memoSqrt(op3))
    )(memoAdd(op1, op2))
  )(memoSquare(x), memoSquare(y))
}

Finally, we can extract the functions to run them through the memoization operation:

const fn1 = memo((op1: number, op2: number) => fn2(memoAdd(op1, op2)));
const fn2 = memo((op3: number) => fn3(memoSqrt(op3)));
const fn3 = memo((op4: number) => op4);

function superMemoDInner(x: number, y: number) {
  return fn1(memoSquare(x), memoSquare(y))
}
const superMemoD = memo(superMemoD, 'd');

While requiring a fancy program rewriting, to the point where the original program is unrecognizable, this has a more aesthetically pleasing property that one can begin to imagine a principled way of adding incrementality instead of manually inserting if-else statements.

Also having so many memoization calls is certainly an overkill in any practical problem – we are memoizing an identity function at some point! – but the point of pushing a simple example to the extreme is to see all the opportunities for incrementality.

However, notice that we still have the same problem as the example with manual if-else statements, we do not have incrementality for this flow:

While we can “skip to the end” of the computation, we cannot skip over the purely x part of the computation graph, if we know x hasn’t changed.

It is likely achievable with more fancy program rewriting, we will get there by using a different technique - push-based incremental computation.

Push vs Pull in Incremental Computation

In the computations we have seen so far the numbers were either directly read through variables x, op1, or we used a .get(): number method. These are examples of pull-based computation, because the code that needs to do something with the numbers pulls them.

There is a dual approach known as push-based computation, because the new values of inputs, push themselves into the computation. A telltale sign of push-based computation is where in the type signature does the core computation type T appear:

• pull - the methods look like (...): T.
• push - the methods looks like ((x: T) => ...): ....

Another terminology used is reactive vs interactive, but there is something called ‘push-based reactivity’ so I am going to steer clear of these to avoid confusion.

In our original example, a push-based version will look something like this:

// description
const x = new Input((o) => op1.set(o));
const y = new Input((o) => op2.set(o));
const op1 = new SingleInputCmp(square, (o) => op3.set1(o));
const op2 = new SingleInputCmp(square, (o) => op3.set2(o));
const op3 = new DoubleInputCmp(add, (o) => op4.set(o));
const op4 = new SingleInputCmp(Math.sqrt, (o) => console.log(`new output ${o}`));

// computation
x.set(1);
y.set(1);

Notice the key difference is that each object is created with a callback that tells it whom to notify upon a change in output. Also the direction of the computation is direct as it progresses from inputs towards outputs.

Writing the underlying classes is relatively straight forward:

class Input {
  constructor(readonly set: (x: number) => void) {}
}

class SingleInputCmp {
  constructor(private readonly cmp: (x: number) => number,
              private readonly update: (x: number) => void) {}
  set(x: number) {
     this.update(this.cmp(x));
  }
}

until we get to the DoubleInputCmp which is required to store some state as the two input updates can arrive at different times.

class DoubleInputCmp {
  lastArg1?: number;
  lastArg2?: number;

  constructor(private readonly cmp: (x: number, y: number) => number,
              private readonly update: (x: number) => void) {}
  set1(x: number) {
      if (this.lastArg2 != null) {
        this.update(this.cmp(x, this.lastArg2));
      }
      this.lastArg1 = x;
  }

  set2(y: number) {
      if (this.lastArg1 != null) {
        this.update(this.cmp(this.lastArg1, y)); 
      }
      this.lastArg2 = y;
  }
}

But once we started adding tracking of state inside the computation nodes, we are basically one step away from incrementality. It will look something like this:

class Input {
  lastValue?: number;
  constructor(private readonly update: (x: number) => void) {}
  set(x: number) {
      if (x !== this.lastValue) {
        this.update(x);
        this.lastValue = x;
      }
  }
}

class SingleInputCmp {
  lastValue?: number;
  constructor(private readonly cmp: (x: number) => number,
              private readonly update: (x: number) => void) {}
  set(x: number) {
      if (x !== this.lastValue) {
        const newVal = this.cmp(x);
        this.update(newVal);
        this.lastValue = newVal;
      }
  }
}

class DoubleInputCmp {
  lastValue1?: number;
  lastValue2?: number;
  constructor(private readonly cmp: (x: number, y: number) => number,
              private readonly update: (x: number) => void) {}
  set1(x: number) {
      if (x !== this.lastValue1 && this.lastValue2 !== undefined) {
        const newVal = this.cmp(x, this.lastValue2);
        this.update(newVal);
      }
      this.lastValue1 = x;
  }

  set2(y: number) {
      if (y !== this.lastValue2 && this.lastValue1 !== undefined) {
        const newVal = this.cmp(this.lastValue1, y);
        this.update(newVal);
      }
      this.lastValue2 = y;
  }
}

Now a recomputation will look like:

y.set(3); 
// 3.1622776601683795 logged
y.set(-1);
// 1.4142135623730951 logged
y.set(1);
// nothing logged, no change.

And by the magic of update callbacks and lastValue checks the computation does the minimum needed work. The downside of this approach is that batch updates, meaning change a number of inputs and then recompute are harder to implement.

Push-based computations appears naturally easier for incrementality. The same observation was made by Yaron Minksy in his excellent blog on the Incremental library in OCaml https://blog.janestreet.com/introducing-incremental/.

If you are wondering if there is such thing as a reversed push-based computation, that’s another thing I am leaving to the reader. Spoiler it doesn’t appear to be nicer than the direct push-based style.

Connection with Reactive / Streaming frameworks

If you are familiar with reactive primitives like - streams, observables, etc, you might have observed that the ‘push-based’ code is starting to look like one. That is absolutely correct, here is the same computation, using rxjs observables.

import {of, combineLatest, Subject} from 'rxjs';
import {map, distinctUntilChanged} from 'rxjs/operators';

const x = new Subject<number>();
const y = new Subject<number>();

const op1 = x.pipe(map(square), distinctUntilChanged());
const op2 = y.pipe(map(square), distinctUntilChanged());
const op3 = combineLatest(op1, op2).pipe(map(([x, y]) => add(x, y)),
    distinctUntilChanged()); 
const op4 = op3.pipe(map(Math.sqrt), distinctUntilChanged());

op4.subscribe(console.log);

console.log('initial computation');
x.next(1);
y.next(1);

console.log('re-computation of with new y');
y.next(-1);

console.log('re-computation of with new x');
x.next(3);

So is incremental computation the same as reactive programming? The way I see it reactive programming with streams can solve many problems of which incremental computation is just one of. As we shall see as we go along incremental computation does not need the full power of Rxjs reactive primitives.

Build systems and incremental computation

Build systems are tools that perform incremental computation specifically in the domain of files and executables that read and write these files. If you familiar with build systems like ‘make’, ‘ninja’ or ‘bazel’, you might have already spotted the similarities with what we have been discussing so far.

The major different is the domain of build tools is more limited than general computation, and usually they have DSL for describing the computation that is different from a general purpose programming language.

Our simple computation will look like this in Make. If you never seen a Makefile before you read it as <output filename>: <input files>\n\t<bash command to run>.

op1: x
	node square.js x > op1

op2: y
	node square.js y > op2

op3: op1 op2
	node add.js op1 op2 > op3

op4: op3
	node sqrt.js op3 > op4

d: op4
	cat op4

The scripts square.js, add.js, sqrt.js are straight-forward implementation that read the files, parse them as numbers and print the operation in the name.

// computation
$ echo 1 > x; echo 1 > y;
$ make d
node square.js x > op1
node square.js y > op2
node add.js op1 op2 > op3
node sqrt.js op3 > op4
cat op4
1.4142135623730951

// recomputation
$ echo 3 > y;
$ make d
node square.js y > op2
node add.js op1 op2 > op3
node sqrt.js op3 > op4
cat op4
3.1622776601683795

As make prints out the operations it performs, it is clear that op1 is skipped when its inputs have not changed. It is worth mentioning that build systems usually use file timestamps as check whether something has changed or not, which can result in less incrementality when using inputs like -1 that are equivalent to 1 after squaring.

In terms of the characteristics we described earlier, make looks like a reverse pull-based computation. We start with the final output op4 (reverse) and each file is directly read (pull-based) instead of using a file watch mechanism for each file to pass it contents into the next operation.

Since, build systems are most successful implementations of incremental computations, one can say that incremental computation is a way of turning your general programs into small build systems.

Onto part 2

The next challenge is to extend the toy computation model to a full blown language that includes control flow and mutable object. We will begin with control flow.

Continue to part 2 of the post