We have been talking about general computation, but so far our language was very limited. We only used function calls, numbers, and simple variable binding.

We will slowly add more language primitives and see how to still have full incrementality of the computation.

Conditional statements

Let’s add a single conditional statement first.

function cond(b: boolean, x: number, y: number) {
  return b ? x * x : y * y; 
}

What does it mean to make cond incremental? Say we compute the result first for some values of b, x, y.

// computation
cond(true, 1, 2);

It would be ideal to skip any work if the recomputation looks like cond(true, 1, 3). The value of y is inconsequential while the first argument is true. However, if b is false the situation is flipped and any change of x should be inconsequential to the computation.

Let’s go over the techniques we learned about in part 1. First it is clear that naive memoization will not work. When going from cond(true, 1, 1) to cond(true, 1, 3) memoization will redo the whole work, while we want to do nothing.

Then we can try to build the computation graph. Breaking down the computation into basic operations we get:

const op1 = x * y;
const op2 = y * y;
const op3 = b ? op1 : op2;

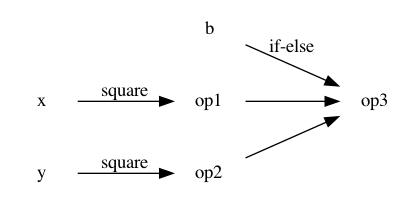
However, this still comes short as changing y means that even if b is always true, the square of y will be computed. This is unavoidable using the techniques we have seen so far.

In order to achieve better incrementality in presence of conditionals, we will have to move to a dynamic model of computations.

Dynamic vs Static computation graph

The right viewpoint is that depending on the last value of b the computation is represented by one of the two following options.

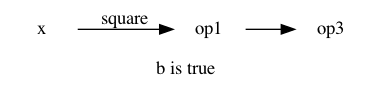
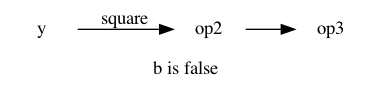
The incremental algorithm should switch between the two options after reading b.

In this example computing b is trivial (it is an input), but in general there could be another sub-computation to get to it.

To fully support incremental computation and conditional statements one needs to have support for a dynamically adjusting computation graph. Otherwise, the static graph techniques can still be used, but they will be an over-approximation. They will basically treat op1 ? op2 : op3 as a function f(op1, op2, op3) that always needs all three inputs.

One has to be careful in using the word dynamic as here we are talking about adjusting the computation graph, not the graph creation itself. As we have seen in part 1, the computation graph implementations we used where build dynamically. We still consider them static incremental computation as they cannot adjust during re-computations.

Unsurprisingly, the same observations were made in the build systems space in the paper Build systems a la carte (see refs in part 3). In their work they used a model for build systems written in Haskell. Our separation between static and dynamic computation graph is equivalent to what they call - applicative vs monadic build systems. Most popular build systems like make are applicative (static).

Adaptive (self-adjusting) computation

While turning the example above into an incremental function is relatively easy using if-else statements (try it), a general framework that supports dynamic incremental computation is too involved to go through in this post.

Luckily, this has been well studied in the past and there existing implementations. The work of Acar - Self-adjusting computation support dynamic incremental computation in OCaml. It was slightly modified and improved by Carlsson in Monads for Incremental Computing. His implementation is in Haskell making heavy use of monads and do-notation. I have translated his implementation to TypeScript - adapt-comp. It required losing some of the heavy monadic type guarantees from the Haskell implementation, but it caries the same basic algorithms and datatypes.

At this point I use the names ‘self-adjusting’, ‘adaptive’ and ‘incremental’ computation interchangeably when talking about the concepts. The library implementing the particular algorithms for incremental computation is called ‘adapt-comp’ in reference to the original work by Acar, et.al.

The distance function example from part 1 of the blog post looks like this using the library:

const x = comp(pure(1));
const y = comp(pure(1));

const op1 = comp(read(x, x => pure(x * x)));
const op2 = comp(read(y, x => pure(x * x)));
const op3 = comp(read(op1, x => 
                 read(op2, y =>
                   pure(x + y))));
const op4 = comp(read(op3, x => pure(Math.sqrt(x)))); 

// computation
console.log(op4.get());

// re-computation
write(y, 3);
console.log(op4.get());

The basic block of adapt-comp are the comp constructor which builds a single build block of the computation. The only argument to comp describes how is the operation built. It either a basic value, which has to be wrapped like this - pure(<some value>), or a result of reading another variable using the read function. Once a variable is read with read, we pass a callback that describes what to do with the value that was just read. The only catch is that at the end of the callback we still have to return another pure or read.

(Aside: if one is familiar with monads they recognize the structure here, which comes from the Haskell linage of this code. If not don’t worry, my exposition is self-contained.)

This is a push-based direct incremental computation using the terminology from part 1, as we observed that it leads to the easiest way to add incrementality. When one calls write(y, 3), all the computations that had read(y, ...) have their corresponding callback retriggered, then recursively their dependents are retriggered, and so on. At any point the last and new values are compared and if the value hasn’t changed the retriggering is stopped.

So far, this doesn’t seems to carry its weight as we had simpler implementations doing this in part 1. However, ‘adapt-comp’ supports a dynamic incremental computation too. Our original dynamic example looks like this in ‘adapt-comp’:

const bVar = comp(pure(true));
const xVar = comp(pure(1));
const yVar = comp(pure(1));

const cond = comp(read(bVar, b => b ? 
                                  read(xVar, x => pure(x * x)) :
                                  read(yVar, y => pure(y * y))));

One convenience is that we no longer had to extract op1 and op2 into separate definitions. There are implicitly objects behind the two read calls that play similar role.

But the real benefit is that the dynamic reads during computing cond are recorded on each computation and recomputation. Since y is not a static dependency of cond, but rather something that was read (or not) as we went along. Thus a recomputation is not triggered when y changes.

write(y, 3);  // does not even recompute y * y
console.log(op4.get());  // immediate return of the previous value

Observable example

As seen in part 1, the observable pattern and in particular RxJS implementation allows for easy implementation of push-based incremental computation (and much more).

To strengthen this point this is how our example will look like in RxJS.

import {of, switchMap, Subject} from 'rxjs';
import {map, distinctUntilChanged} from 'rxjs/operators';

const b = new Subject<boolean>();
const x = new Subject<number>();
const y = new Subject<number>();

const op1 = x.pipe(map(square), distinctUntilChanged());
const op2 = y.pipe(map(square), distinctUntilChanged());
const op3 = b.pipe(switchMap(b => b ? op1 : op2));

op3.subscribe(console.log);

// initial computation
b.next(true);
x.next(1);
y.next(1);

// re-computation of with new y
y.next(3);  // no log occurs

// re-computation of with new x
x.next(3);  // log 9 occurs

(Aside for readers familiar with monads: you might remember that build systems article called systems supporting dynamic computation graphs – monadic. It is not a coincidence that we had to use the switchMap operator here, which indeed has the monadic interface).

If feels natural to do for and while loops next, but actually more primitive concept is recursion.

Recursion

We have been focusing on a single function so far. Extending the framework to multiple distinct functions is straight forward. Graphically, a function call was treated as a single node, but if it is an incremental computation we can embedded its own graph into another node to form one bigger computation graph.

The question of multiple calls into the same function, especially recursively might give us a pause. Say we want to make the following recursive function incremental:

function f(x: number, y: number) {
  if (x <= 0) {
    return y; 
  }
  return f(x - 1, x + y);
}

The intermediate step is to write it in the form of simple operations and conditionals:

function f(x: number, y: number) {
  const nextX = x - 1;
  const nextY = x + y;
  const lessZ = x <= 0;
  return lessZ ? y : f(nextX, nextY);
}

f(10, 0);  // returns 55;

Now we can use the adapt-comp library to directly translate:

// description
function f(x: Modifiable<number>, y: Modifiable<number>): Mod<number> {
  const nextX = comp(read(x, x => pure(x - 1)));
  const nextY = comp(read(x, x => read(y, y => pure(x + y))));
  const lessZ = comp(read(x, x => pure(x <= 0)));
  return comp(read(lessZ, b => b ? read(y) : read(f(nextX, nextY)))); 
}
const x = comp(pure(10));
const y = comp(pure(0));

// computation
const res = f(x, y);
res.get();  // returns 55;

// re-computation
write(y, 100);
res.get();  // returns 155;

As we see there is nothing special about recursion, because we can dynamically create new computation variables. The function boundaries are almost irrelevant for the re-computation. The only thing that matters is which computations are created by comp and what reads have happened during the computation.

Looping and Mutable variables

Finally, we can get to for and while loops. Unfortunately, we cannot directly support for and while loops in the adapt-comp world. Calling comp in a loop by itself is fine, but we cannot interleave the termination control flow from the read callbacks back to original loop.

However, we are in luck as all for and while loops can be rewritten through recursion. In fact the recursion example above could be seen as the functional rewrite for the following imperative program:

function sumUp(x: number, y: number) {
  let acc = y;
  while (x <= 0) {
    acc += x; 
  }
  return acc;
}

So we already have an incremental solution for it above.

This example, also shows one of the failures of incremental computation, by virtue of it being so general, it does not take into account the algebraic properties of + (commutativity, associtivity, etc.)

If we recompute sumUp(10, 100) after sumUp(10, 0) it is clear to us that the best way to do it is through simply adding 100 to the old result. But the incremental program we have above sees the computation as:

(100 + ... + (3 + (2 + (1 + (0 + 0))))) 

where the last 0 is y. Changing it to 100 busts the whole chain of computation and all additions get redone. We know that doesn’t seem efficient, the incremental computation show just add 100 to the previous result.

Now that is not unavoidable as one can write the computation using the algebraic properties of +:

(100 + ... + (3 + (2 + (1 + 0)))) + 0

But an automated framework cannot do that without some knowledge about the properies of +. The user herself can write the computation in that form from the beginning, but that goes against the promise that the incremental program is easily extracted by code transformation from from the original computation.

Moreover, once the user has to think about incrementality they can write by hand this update function for sumUp:

function updateSumUpForNewY(oldSum: number, deltaY: number) {
   return oldSum + deltaY;
}

const sum = sumUp(10, 0);
const updateSum = updateSumUpForNewY(sum, 100 - 0);

This leads to a completely new way of viewing incremental computation, inspired by the mathematics of differences. Instead of merely tracking which input and computation has changed and which has not, we can extend the model to add information on how has the input changed.

The Computational Derivative

To move to an even more mathematical notation, if the original function is f(x, y) and we want to compute f(x', y'), an incremental way of computing it would be to use f(x, y) ⊕ f'(x, y, Δx, Δy)) where Δx = x' ⊖ x and Δy = y' ⊖ x. The reads roughly as ‘to compute the new output, we add the old output to the result of some special function f' that consumes the old inputs and their changes’.

Why the circles around + and -? Because we didn’t specify the types these are generic ways of creating ⊕, and applying ⊖ diffs for some given type. For number as the input type, these are literally + and - and the diff type is number. However, for number[] the diff structure will have to be more complicated. One-way to model it is using diffs as {additions: {idx: number, newVal: number}[], deletions: number[]}, where ⊕ and ⊖ apply or extract these diffs onto number arrays.

What about f'? That’s the computational derivative. If we can have that function in a form that it is cheaper to compute than the original f, we have succeeded at the goals of creating an incremental computation.

In our example above sumUpTo' is

function sumUpTo'(newX: number, newY: number, deltaX: number, deltaY: number) {
  return (2 * newX - deltaX + 1) / 2 - deltaY;  
}

Of course, I cheated in creating this by applying well-known mathematical equalities (check my work). The question of interest is how to extract that from the original function definition. Can this be done for any general computation, not just numerical?

Deriving such derivative function in the lambda calculus is described in the paper A Theory of Changes for Higher-Order Languages. It includes a prototype Scala implementation, which I have not had a chance to explore further. On the practical side the OCaml Incremental library has added support for diffable data Self Adjusting DOM and Diffable Data, specifically for mutable data structures that we will explore in a bit.

It is unclear to me whether the diffable addition to incremental computation is objectively different approach compared to the basic methods we have discussed for far or an optimization to support the pragmatics of mutable data structures. Let me know what do you think.

Automatic-differentiation aside

If you have been following you the machine learning community this might light-bulb - automatic differentiation!

Unfortunately, the computational derivative for a function that deals with numerics is not the same as the mathematical derivative for the underlying math function. Mathematically, the computational derivative is just the difference function f(x') - f(x). Different forms of writing that function (with some being faster to compute) is question in the domain of computer science and not mathematics.

That said the study of applying program transformations to extract the mathematical derivative has a lot of parallels with the techniques for incremental computation. The paper Demystifying Differentiable Programming: Shift/Reset the Penultimate Backpropagator is a great overview on the subject.

Data structures

You might have noticed that all the functions so far only dealt with numbers. That was intentional, as adding lists and maps to incremental computation, will present another divergent point.

One way we can approach this problem is sticking to the purely functional paradigm. We can build lists out of pairs of value and a next pointer, and trees as value with two pointers. Using the adapt-comp library again and its core Modifiable<T> type, these structures can be written as:

interface IncrementalList<T> {
  readonly value: T;
  readonly next: Modifiable<IncrementalList<T>>;
}

interface IncrementalTree<T> {
  readonly value: T;
  readonly left: Modifiable<IncrementalTree<T>>;
  readonly rigth: Modifiable<IncrementalTree<T>>;
}

Finally, a Map<K,V> API can be added as implemented by lists of entries or a balanced tree using standard functional constructions.

Once we have data structures, we can add algorithms. For example, this is how incremental quick sort looks like - aqsort.ts. The incremental version of the quick sort takes on average O(log n) to update for a single new insertion.

As this example show, embedding incremental computation into a non-computation language like JS is possible, but unnatural. We have to rebuild a mini-functional language by avoiding the built-in control flow and data structures.

The alternative is to provide a bridge with the mutable world where data structures are not built out of incremental bindings. That brings us back to the differential model where data structures come with their own definitions of deltas (also called diffs), computing deltas, applying deltas, and propagating them incrementally though all methods.

For example, Jane street’s incremental has diffing extensions for maps and unordered arrays, to support Ocaml’s native maps and list in a more fine grained way than treating them as opaque objects that either change or not.

Incremental records

Records represent one of the easiest data structures to incrementalize. Because they are not statically changing structure like lists and maps.

Consider the following example:

interface Person {
  name: string;
  addres: string;
}

type Incremental<T> = {[key in keysof T]: Modifiable<T[key]>};

const p: Incremental<Person> = {name: comp(pure('John Smith')), address: comp(pure('neverland'))};
const businessCard = comp(read(p.name, n => read(p.address, addr => pure(`${p} at ${addr}`))));

// computation
businessCard.get();

// recomputation
write(p.name, 'Jane Smith');
businessCard.get();

The salsa framework in Rust relies on this observation to only support static object definitions. Through macros a lot of the supporting machinery is generated on predefined functions instead of being as dynamic as the incremental implementations above. An extra layer of extensibility is added through supporting keys per object - think p['John Doe'].name. As long as there are no methods working over the collection as a whole (no map, reduce, etc) this is a simpler model than general incremental computation, but still expressive enough to help with writing incremental compilers.

Online combinatorial algorithms

You might wonder what is the downside to adding the differential view since it lets us use more complicated data structures and methods on them. The problem is that at the low level we only have a handful a primitives, once we start climbing up the abstraction stack there is a whole zoo of data structures and methods that have to be supported.

At the extreme there are fully custom data structures that support very efficient results to a fixed set of computations, after small changes. This work of Tarjan is representative - [A Data Structure for Dynamic Trees] (https://www.cs.cmu.edu/~sleator/papers/dynamic-trees.pdf). One of the original goals of research of incremental computation was to automatically derive these type of structures through incrementalizing the classical algorithms, instead of incremenlizing them one by one.

Onto part 2

This concludes the introduction into incremental computation, in part 3 we will talk about applications to UI programming and conclude the series.

Continue to part 3 of the post