Is this JS function pure?

In 2019, as functional programming was making the last inroads dethroning OOP, I kept hearing the mantra of “just use pure functions” in JS. Something didn’t sit right with me when talking very deterministically about pure functions in a large unpure language like JS. Especially, after seeing JS tooling perform optimizations based on a pure annotation (like webpack).

While everyone agrees x => x + 2 is pure, I felt there are a lot of subtle situations where disagreements might arise. What is worse than terms with imprecise meaning is terms with imprecise meaning where people using them are not aware there is imprecision.

Wikipedia defines pure function as a function that:

returns identical values for identical arguments.
has no side-effects (no mutation of non-local variables, mutable reference arguments or input/output streams).

So I ran a twitter poll with 10 not so obviously pure (or not) functions. This blog post is a summary of that poll and results amongst the 383 respondents (presumably most JS developers that follow me).

Question 1

function f() {
    return Math.random();
}

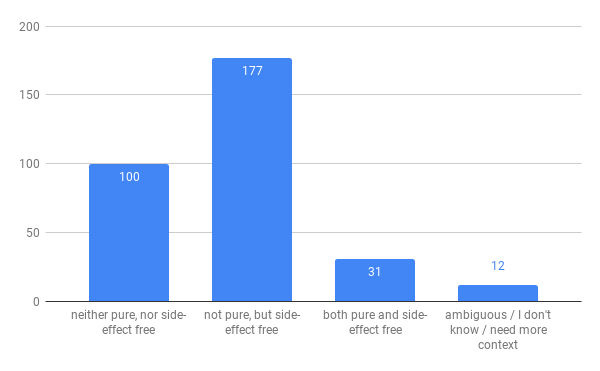
Q1 answers

My take - clearly fails the first property for pure, so impure. Whether it has a side-effect, is surprisingly subtle, and depends on whether one sees the internal change of the pseudorandom number generator as a side-effect or not. Appears my audience was similarly split on the side-effect question.

Question 2

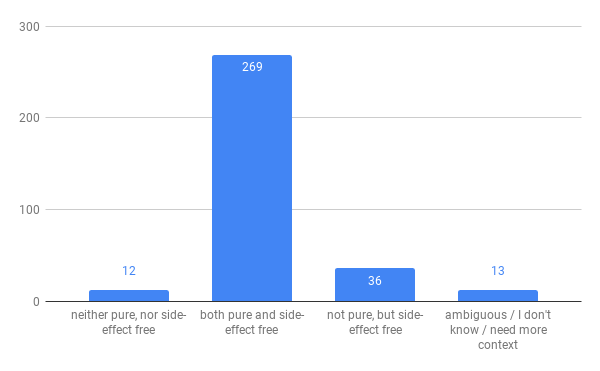
function f() {
    return [0];
}

My take - this example forces one to confront the fact that in the definition of pure, we need to pick a definition of equality. JavaScript only has referential equality build in, so to me it would be the only reasonable choice, hence not pure. This was a minority view amongst the replies.

Q2 answers

Question 3

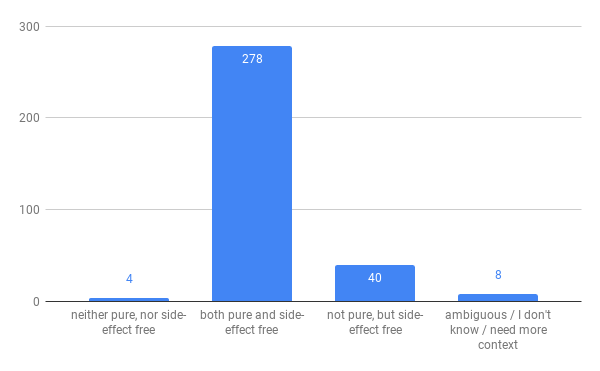
function f() {
    return () => 0;
}

My take - A variation of Q2. My answer would be the same. I was hoping the structural equality crowd to get a bit less comfortable here - what would “structural equality” mean for functions. I could have pushed this further towards extensional and intentional equality for functions - are (a) => a + a and (a) => 2 * a equal as pure functions. What about (a) => a vs (b) => b?

Q3 answers

Question 4

function f() {
    throw 'oops';
}

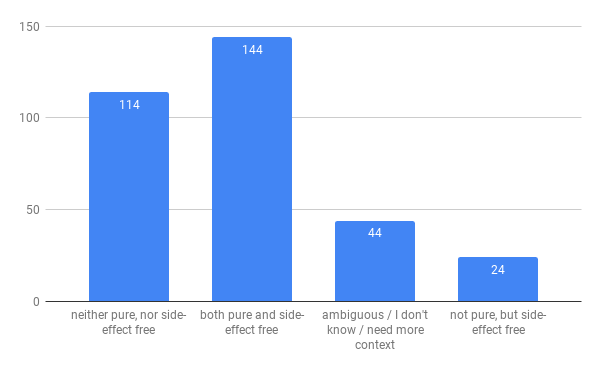
Q4 answers

My take - is throwing an error a side-effect or just an alternative “return” value? I tend to think the former. The responses were very split here.

Somewhat hilariously, I just noticed that I wrote return throw 'oops' in the original post, which is a syntax error in JS, and a whole different can of worms, especially if a static analyzer is trying to determine purity on code that might contain errors.

Question 5

function f(x) {
    // DEBUG_FLAG is usually false.
    if (DEBUG_FLAG) {
        console.log('debug', x);
    }
    return 2 * x;
}

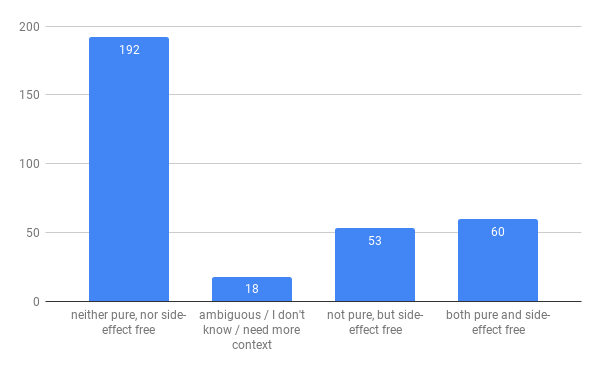
Q5 answers

My take - logging is pretty canonically accepted as a side-effect, but I threw in some wrinkle around DEBUG_FLAG, to add extra confusion around the effect potentially not occurring. There is an extra layer of provocation on whether “pure” is a statically determinable property, or a runtime attribute of a particular invocation (depending on the state of the DEBUG_FLAG at the particular invocation). Finally, reading a variable like DEBUG_FLAG in JS can be seen as a side-effect (later questions also explore that).

Question 6

const y = 0;

function f() {
    return y;
}

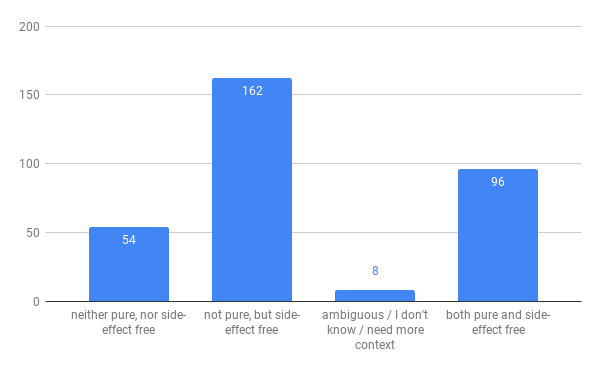
Q6 answers

My take - Is reading a non-local const variable a side-effect? I lean yes, but there were some folks that disagreed with this.

Question 7

// only f has access to _memoize.
const _memoize = new Map();

function f(x) {
    if (_memoize.has(x)) {
        return _memoize.get(x);
    }
    let res = 2 * x;
    _memoize.set(x, res);
    return res;
}

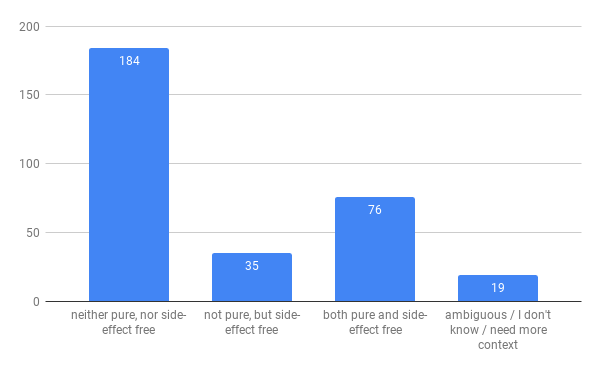
Q7 answers

My take - despite what the comment tries to convince you, the map is a non-local object that has observable change, so this is an impure function.

Question 8

function f(x) {
    // only f mentions _privateProp
    x._privateProp = 0;
    return x;
}

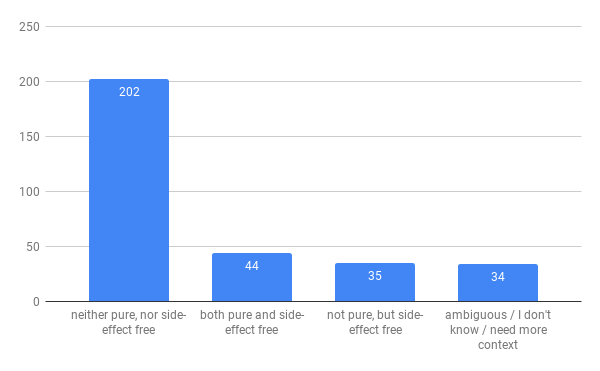
Q8 answers

My take - same as Q7, the principled answer is non-local mutation is happening so impure (even if no one is observing it)

Question 9

function f(obj) {
    return obj.someProp
}

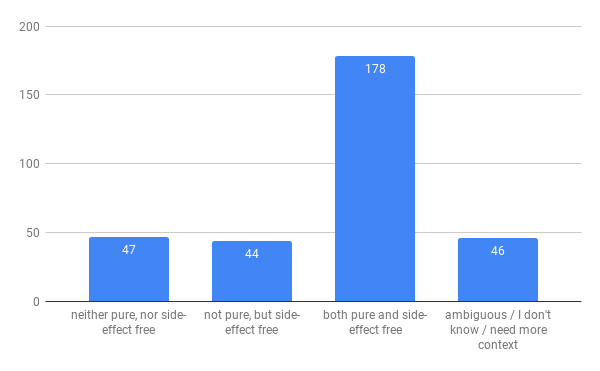
Q9 answers

My take - consistently using referential equality, this function can return different results for equal inputs. Reading a property can be seen as a side-effect as JS allows for getter methods. The survey responders did not agree, and overwhelmingly declared this function pure.

Question 10

const A_REGEXP = /abc/g

function f(x) {
    return A_REGEXP.test(x);
}

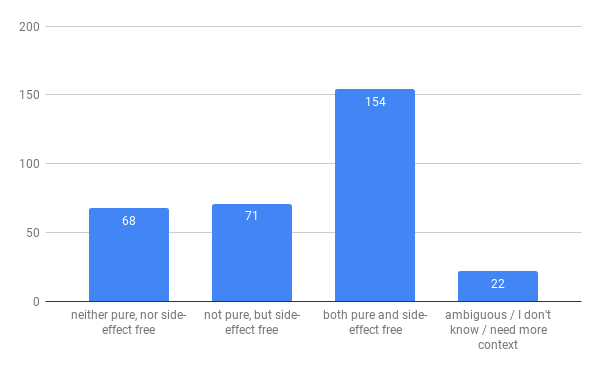
Q10 answers

My take - a bit of a gotcha, but turns out regexps in JS mutate state on the global RegExp object, so this function has side-effects.

Takeaways

This survey reveals that “pure function” means different things to different JavaScript developers. Among the 383 respondents, there was significant disagreement on nearly every question, showing that the term is far fuzzier than most realize.

The core issue is that “pure function” is a theoretical computer science concept being applied to a practical programming language that wasn’t designed with purity in mind. JavaScript’s spec doesn’t define “pure function” - we’re borrowing an idealized mathematical concept and trying to map it onto a complex, real-world language.

This creates several problems:

Equality is ambiguous. The definition requires “identical values for identical arguments,” but JavaScript only has referential equality built-in. Should [0] equal [0]? What about two functions that do the same thing? There’s no universally agreed answer.

Side effects are hard to define. Is reading a global constant a side effect? Is throwing an error? Is mutating a private property that no one else observes? The survey shows people draw the line in different places.

The language works against us. JavaScript has surprising gotchas (like stateful regexps) and allows side effects in unexpected places (like getter methods). Pure functions exist on a spectrum from “close to the mathematical ideal” to “far from it,” but there’s no clear threshold.

When someone says “just use pure functions” in JavaScript, they’re really advocating for writing code that stays closer to idealized mathematical models. That’s good advice, but the model will never perfectly match reality. Instead of treating purity as a binary property, it’s more useful to think about how and why a function deviates from the ideal - and whether those deviations matter for your use case.